SWEEET – Module 2
2. Locational Marginal Price (LMP)
The second section consists of a brief introduction to Locational Marginal Pricing in module 2; module 2a consists of excel input values and output solution to the problem discussed in module 1; module 2b is the guide leaflet for 2a.
Locational Marginal Price at a node in the network is the marginal cost of the generation source to deliver one additional unit of energy. This price is determined considering that at this node energy source is already deployed by a generation source. LMP is a method for wholesale electric energy prices to reflect the value of electric energy at different locations, accounting for the patterns of demand, generation, and the physical constraints of the transmission system. Prices in LMP-based wholesale power markets vary by location and time and reflect the incremental cost of meeting demand at any location at any point in time.
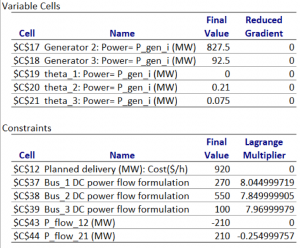
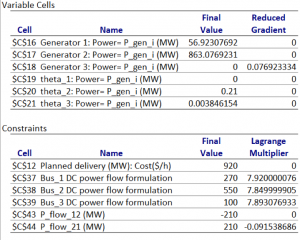
Consider the example shown in DCOPF module. Excel solver is used to calculate the values for our DCOPF model. Solving the model using “simplex LP/ GRG Nonlinear” function and setting the decision variables as generator dispatch, phase angles and subject to the constraints mentioned in the OPF module, we obtain the DC optimal power flow. The sensitivity report of our model gives us the LMP values as the shadow prices/Lagrangian Multiplier where the Langrangian multiplier is a dual variable.
The solver will give out the optimized values for the mathematical formulation. The values of p1, p2 and p3 are in MW and values of θ1, θ2 and θ3 are in radians.
2a. LMP – Excel sensitivity report
Output – (Case 1 – 2 Generators)
Output – (Case 2 – 3 Generators)
2b. Excel input/output for LMP
Continuing from step 7, now –
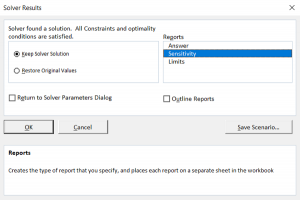
Step 8 – This window will pop-up after selecting solve. Select “Sensitivity” in Reports section and click OK to view the sensitivity report.
The sensitivity report given by the solver shows us all the values of decision variables as well as constraints. It also shows the value of Lagrange multiplier which is the LMP in our case. This Lagrangian multiplier is a dual variable.